Performance of various square root computing algorithms
After reading a post on fast integer square roots on Robert Basler’s blog I got curious about performance of those algorithms on modern hardware. The most famous is of course the “Quake 3 invsqrt”. I’ve also tested two algorithms mentioned on Stack Overflow.
My microbenchmark approach was basically to compute sum of square roots from 1 to 1e9 into a UINT64 variable. loops is 1e9.
// math.h double sqrt
QueryPerformanceCounter(&pc1);
UINT64 uu = 0;
for (UINT32 i = 0; i < loops; i++)
{
uu += (UINT64)sqrt((double)i);
}
QueryPerformanceCounter(&pc2);
elapsed = (pc2.QuadPart-pc1.QuadPart)/(double)freq.QuadPart;
wprintf(L"Sqrt double: %.3fms (%u)\n", elapsed*1000.0, uu);
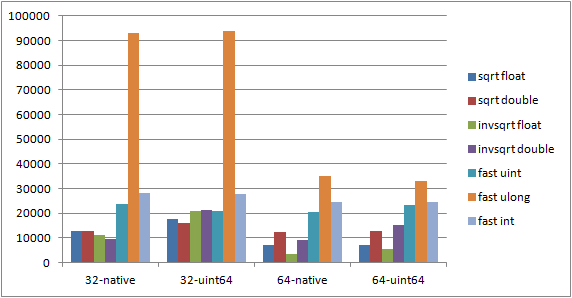
Results from my laptop (DualCore Intel Core i7 620M, 2666 MHz (20 x 133), times in milliseconds):
Long double sum of sqrts: 21081851051977.781000 32bit: Sqrt float: 17741.012 (1652390483) Sqrt double: 16131.129 (1651579237) Fast uint sqrt: 20723.943 (1651579237) Fast ulong sqrt: 93737.070 (1651579237) Fast int sqrt: 27791.603 (2558293500) Fast Q3 float sqrt: 20919.534 (3883084482) Fast Q3 double sqrt: 21357.330 (3882261863) 64bit: Sqrt float: 7135.535 (1652359905) Sqrt double: 12613.416 (1651579237) Fast uint sqrt: 23390.084 (1651579237) Fast ulong sqrt: 32878.867 (1651579237) Fast int sqrt: 24430.502 (2558293500) Fast Q3 float sqrt: 5352.906 (3883079922) Fast Q3 double sqrt: 15216.076 (3882257735)
Compiled as speed-optimized release using VC2010. Enabling SSE/SSE2 didn’t produce noticeable differences. Using fast floating-point model over precise or strict does improve built-in sqrt function performance (as well as Q3’s invsqrt) but I chose to stick to precise model since it’s the default. static_cast had the same performance as C-style casts. Numbers in parentheses are integer sqrt sums, as you can see they vary wildly due to different accuracy of the algorithms.
64bit executable is pretty much always faster, especially for floats. Casting to UINT64 is slower on 32bits of course, but using UINT32 doesn’t change much (tested that as well, minimal differences). Built-in sqrt is still fastest except for float version of Q3’s invsqrt, which is blazingly fast and still very accurate.
Also, a small quiz: why the times increase twofold on FP sqrts if I remove the (UINT64) cast in the inner loop (hint: look at the sum)?
(32bit, but it's similar for 64bit) uu += sqrt((float)i); Sqrt float: 41906.894 (1652612419)
To check how much casting the results to integer affects performance I also did test without it: sqrt functions returning double were summed to a double variable (same with floats). Results below:
Long double sum of sqrts: 21081851051977.781000 32bit: Sqrt float: 12666.459 (549755813888.000000) Sqrt double: 12647.830 (21081851051977.781000) Fast uint sqrt: 23757.851 (1651579237) Fast ulong sqrt: 92842.952 (1651579237) Fast int sqrt: 28243.427 (2558293500) Fast Q3 float sqrt: 11077.491 (549755813888.000000) Fast Q3 double sqrt: 9390.088 (21062606916280.066000) 64bit: Sqrt float: 7151.176 (549755813888.000000) Sqrt double: 12596.555 (21081851051977.781000) Fast uint sqrt: 20426.025 (1651579237) Fast ulong sqrt: 35248.122 (1651579237) Fast int sqrt: 24476.170 (2558293500) Fast Q3 float sqrt: 3429.053 (549755813888.000000) Fast Q3 double sqrt: 9192.112 (21062606916106.129000)
Integer sqrts are unaffected since they didn’t have casts anyway. Built-in sqrt is much faster now, but it’s outperformed by the invsqrt for doubles (and floats on x64)! Something to consider if you don’t need very accurate numbers (it’s still pretty damn accurate).
32-native: 32bit executable with sqrts summed to native types (without casts)
32-uint64: 32bit executable with sqrts summed to UINT64
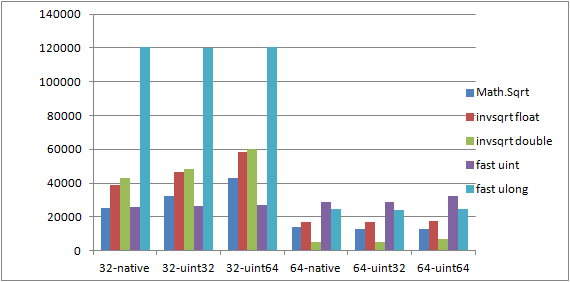
I wouldn’t be myself if I didn’t test the same algorithms in C#. Both “fast uint” and “fast ulong” algorithms translate without changes. Q3’s invsqrt just needs unsafe context to use pointers for bit conversions (using BitConverter is slooow). Results? Might surprise you 😉 (using .NET 4.0)
32bit summing to UINT64: Sqrt double: 42939 (21081351068005) Fast uint sqrt: 26769 (21081851045129) Fast ulong sqrt: 120578 (21081851045129) Fast Q3 float sqrt: 58303 (21062106914641) Fast Q3 double sqrt: 60314 (21061877534026) 64bit summing to UINT64: Sqrt double: 12597 (21081351068005) Fast uint sqrt: 32374 (21081851045129) Fast ulong sqrt: 24520 (21081851045129) Fast Q3 float sqrt: 17643 (21062107732210) Fast Q3 double sqrt: 6810 (21061877534026) 32bit summing to native types: Sqrt double: 25200 (21081851051977.8) Fast uint sqrt: 26084 (2151556361) Fast ulong sqrt: 120248 (21081851045129) Fast Q3 float sqrt: 38560 (5.497558E+11) Fast Q3 double sqrt: 42891 (21062377537121.3) 64bit summing to native types: Sqrt double: 13952 (21081851051977.8) Fast uint sqrt: 28848 (2151556361) Fast ulong sqrt: 24573 (21081851045129) Fast Q3 float sqrt: 17068 (5.497558E+11) Fast Q3 double sqrt: 5147 (21062377537121.3)
And as an appendix, source of all the algorithms used:
| Square root microbenchmark code | Show |
|---|---|

Good job Sir
Dude, that’s awesome! The spikes for ulong on 32-bit platforms is rather shocking. I need to rethink my use of 64-bit math.
Hey, I remember a post where you were tackling with action dispatcher on Artemis, we´ve just added three types of queue systems, it may help you! https://github.com/thelinuxlich/artemis_CSharp/commit/85436fb154f1cec527829727ac2175a9b4048a82
Nice! I’ll check it out.